Таблицы истинности логических функций и их построение

Логическая функция одно из основополагающих понятий математической логики. Она зависит от логических переменных и принимает значения из множества, от которого находится в зависимости. Логические функции булевых переменных могут принимать только два значения – 1 или 0.
Понятие таблиц истинности
Задаваться логическая функция может числовым способом, словесным описанием, картами Карно, аналитическим выражением и с помощью таблиц истинности. В последнем случае все аргументы функции следует записать в левой части таблицы, а значения, которые им соответствуют, в правой.
Определения 1 — 2
Таблица истинности – это таблица, просто и наглядно показывающая, какие значения будут у логического выражения при всевозможных наборах переменных функции.
Равносильными именуют те логические выражения с совпадающими последними столбцами таблицы истинности. Обозначают равносильные функции знаком «=».
Правила того, как следует проводить построение таблицы истинности
Несоблюдение хотя бы одного из них ведёт к очень грубой ошибке. Вот эти правила:
- Число строк таблицы должно совпадать с числом комбинаций всевозможных n логических переменных, то есть быть равным 2 n ;
- Количество столбцов таблицы должно равняться сумме числа логических переменных и числа логических операций;
- В построенный шаблон таблицы истинности должны вписываться все значения исходных переменных;
- Построение таблицы истинности выражения происходит по её столбцам, при этом обязательно учитываются правила логических операций.
Порядок действий при построении таблицы истинности для логических выражений
Порядок действий при построении таблицы истинности, какой бы ни была логическая функция, следующий:
- Определить, какое число строк и столбцов будет в будущей таблице. Делается подобное по формулам
X = n + m, Y = 2 n +1.
Где n – число переменных, m – чило логических операций. - Заполнить самую верхнюю строку таблицы переменными и логическими операциями, идя слева направо. При этом приоритетность логических операций следует учитывать обязательно, иначе получится совсем не то, что нужно;
- В первых столбцах перечислить всевозможные комбинации входных значений;
- Выполняя заданные логические операции, заполнить все оставшиеся ячейки;
Ответом следует считать последний заполненный столбец таблицы.
О порядке логических операций
Лучше его представить списком. Логические операции выполняют в следующей последовательности: сначала идёт инверсия, затем конъюнкция, после этого дизъюнкция, после неё импликация, по её выполнении эквиваленция.
После них идут Штрих Шеффера и Стрелка Пирса. Первым может быть выполнено как то, так и другое.
Далее приведём несколько поучительных задач на построение таблиц истинности
Задачи 1 — 3
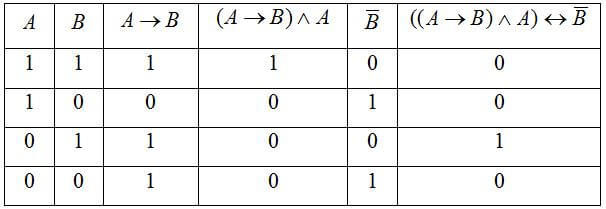
Сделать построение таблицы истинности для функции ((A→B) ∧ A) ↔ B
-
- Определяем сколько будет у нас столбцов. Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6.
- Определяем, сколько будет у на строк. Оно равно 2 n , плюс ещё одна строка для обозначения переменных и логических операций. У нас будет 2 n +1 = 2 2 + 1= 5;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В двух первых столбцах записываем возможные значения переменных;
- В далее идущих столбцах записываем, какие значения принимают промежуточные функции;
- В самом последнем из столбцов записываем итоговые значения функции.
В результате всего этого у нас должно получиться:
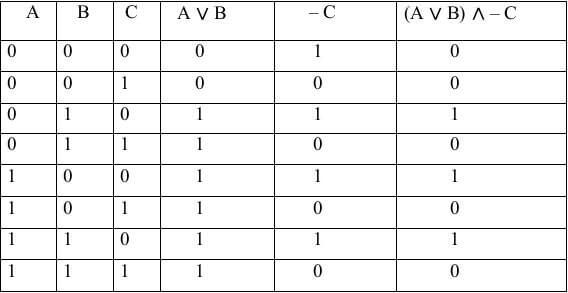
Провести построение таблицы истинности функции (A ∨ B) ∧ – C
- Определяем сколько будет столбцов. Количество переменных у нас 3, количество логических операций 3. Складываем то и другое: 3+3 = 5.
- Определяем, количество строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций.В итоге будет 2n+1 = 2 3 + 1= 9;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В два первые столбца вносим возможные значения наших переменных;
- В далее следующие столбцы записываем, какие значения принимают промежуточные функции;
- В последнем столбце записываем итоговые значения функции.
В итоге получим таблицу:
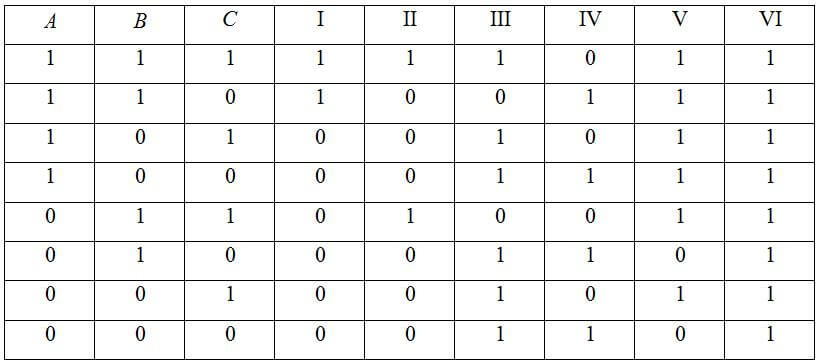
Сделать таблицу истинности для
(A ∧ B ↔ B ∧ C) ∨ (C → A)
Функция посложнее и таблица получится значительно больше, чем предыдущая.
- Считаем столбцы. Количество переменных 3, количество логических операций 6. Значит столбцов будет 3+6=9;
- Считаем строки. Их количество будет 2 3 +1= 9;
- Заполняем первую строку таблицы;
- В первых столбцах записываем все допустимые значения наших переменных;
- В остающихся столбцах пишем, какие наша функция принимает промежуточные значения
- В последний столбец пишем итоговые значения данной нам функции.
В итоге у нас получается таблица:
Нет времени решать самому?
4.3. Логические функции и таблицы истинности
Соотношения между логическими переменными и логическими функциями в алгебре логики можно отобразить также с помощью соответствующих таблиц, которые носят название таблиц истинности. Таблицы истинности находят широкое применение, поскольку наглядно показывают, какие значения принимает логическая функция при всех сочетаниях значений ее логических переменных. Таблица истинности состоит из двух частей. Первая (левая) часть относится к логическим переменным и содержит полный перечень возможных комбинаций логических переменных А, В, С… и т. д. Вторая (правая) часть этой таблицы определяет выходные состояния как логическую функцию от комбинаций входных величин.
Например, для логической функции F = A v B v C (дизъюнкции) трех логических переменных А, В, и С таблица истинности будет иметь вид, показанный на рис. 4.1. Для записи значений логических переменных и логической функции данная таблица истинности содержит 8 строк и 4 столбца, т. е. число строк для записи значений аргументов и функции любой таблицы истинности будет равно 2 n , где п – число аргументов логической функции, а число столбцов равно п + 1.
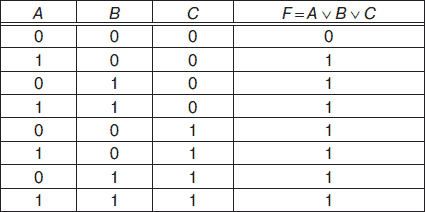
Рис. 4.1. Таблица истинности для логической функции F = A v В v С
Таблицу истинности можно составить для любой логической функции, например, на рис. 4.2 приведена таблица истинности логической функции F = A ? B ? C (эквиваленции).
Логические функции имеют соответствующие названия. Для двух двоичных переменных существует шестнадцать логических функций, названия которых приведены ниже. На рис. 4.3 представлена таблица, в которой приведены логические функции F1, F2, F3, … , F16 двух логических переменных A и В.
Функция F1 = 0 и называется функцией константы нуля, или генератора нуля.
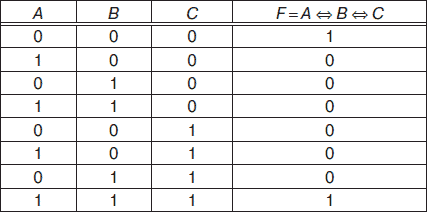
Рис. 4.2. Таблица истинности для логической функции F = A ? B ? C
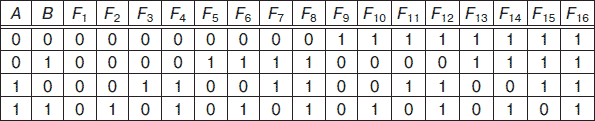
Функция F2 = A & B называется функцией конъюнкции.
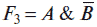
называется функцией запрета по логической переменной А.
Функция F4 = А называется функцией повторения по логической переменной А.

называется функцией запрета по логической переменной В.
Функция F6 = В называется функцией повторения по логической переменной В.
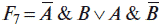
называется функцией исключающее «ИЛИ».
Функция F8 = A v В называется функцией дизъюнкции.
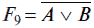
называется функцией Пирса.
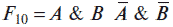
называется функцией эквиваленции.
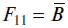
называется функцией отрицания (инверсии) по логической переменной В.
Функция F12 = B ? A называется функцией импликации B ? A.
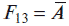
называется функцией отрицания (инверсии) по логической переменной А.
Функция F14 = A ? B называется функцией импликации A ? B.
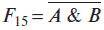
называется функцией Шеффера.
Функция F16 = 1 называется функцией генератора 1.
Среди перечисленных выше логических функций переменных можно выделить несколько логических функций, с помощью которых можно выразить другие логические функции. Операцию замены одной логической функции другой в алгебре логики называют операцией суперпозиции или методом суперпозиции. Например, функцию Шеффера можно выразить при помощи логических функций дизъюнкции и отрицания, используя закон де Моргана:
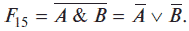
Логические функции, с помощью которых можно выразить другие логические функции методом суперпозиции, называются базовыми логическими функциями. Такой набор базовых логических функций называется функционально полным набором логических функций. На практике наиболее широко в качестве такого набора используют три логических функции: конъюнкцию, дизъюнкцию и отрицание. Если логическая функция представлена с помощью базовых функций, то такая форма представления называется нормальной. В предыдущем примере логическая функция Шеффера, выраженная через базовые функции, представлена в нормальной форме.
При помощи набора базовых функций и соответствующих им технических устройств, реализующих эти логические функции, можно разработать и создать любое логическое устройство или систему.
В настоящее время существует достаточно много программных продуктов, с помощью которых можно реализовать различные логические функции и форму их представления, например в виде таблиц истинности. Логические функции широко используются и в программе MS Excel. Для вызова этих функций необходимо выполнить следующие команды: [Кнопка Пуск – Программы – MS Office ХР – Microsoft Excel] и далее команду: [Вставка – Функция]. В открывшемся окне (рис. 4.4) «Мастер функций – шаг 1 из 2», выберем: «Категория: „Логические“ и далее можно выбрать необходимую логическую функцию: ЕСЛИ, И, ИЛИ, ИСТИНА, ЛОЖЬ, НЕ. В этом же окне можно получить справку по каждой из этих функций.
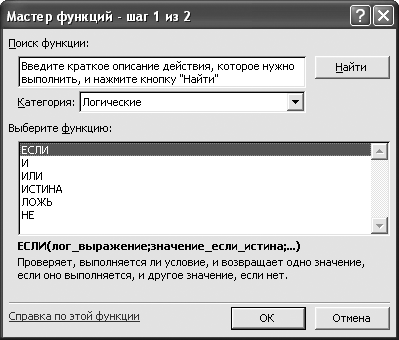
Рис. 4.4. Диалоговое окно «Мастер функций – шаг 1 из 2»
Как видно из рис. 4.4, в состав логических функций программы MS Excel входит функционально полный набор логических функций, состоящий из следующих логических функций: И (конъюнкция), ИЛИ (дизъюнкция), НЕ (отрицание). Таким образом, с помощью функционально полного набора логических функций программы MS Excel можно реализовать другие функции. Логическая функция ЕСЛИ (импликация), также входящая в логические функции MS Excel, выполняет логическую проверку и в зависимости от результата проверки выполняет одно из двух возможных действий. В данной программе она имеет следующий формат: = ЕСЛИ (арг1;арг2;арг3), где арг1 – логическое условие; арг2 – возвращаемое значение при условии, что значение аргумента арг1 выполняется (ИСТИНА); арг3 – возвращаемое значение при условии, что значение аргумента арг1 не выполняется (ЛОЖЬ). Например, если в произвольную ячейку листа программы MS Excel ввести выражение « = ЕСЛИ (А1 = 5; „пять“; „не пять“)», то при вводе числа 5 в ячейку А1 и нажатии клавиши «Enter» в ячейке А1 автоматически будет записано слово «пять», при вводе любого другого числа в ячейку А1 в ней запишется слово «не пять». Как уже отмечалось, с помощью логических функций программы MS Excel можно представить другие логические функции и соответствующие им таблицы истинности.

Рис. 4.5. Реализация модифицированной таблицы истинности логической функции F = A & В
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
Логические функции XPath
Логические функции XPath XPath также поддерживает следующий набор логических функций:• boolean(). Приводит аргумент к логическому значению;• false(). Возвращает false (ложь);• lang(). Проверяет, совпадает ли язык, установленный в атрибуте xml:lang, с языком, переданным в функцию;• not().
Логические операторы
Логические операторы Логические операторы выполняют действия над логическими значениями. Все они приведены в табл. 14.5. А в табл. 14.6 и 14.7 показаны результаты выполнения этих операторов.Основная область применения логических операторов — выражения сравнения (о них см.
Логические функции определения типа переменной
Логические функции определения типа переменной is_scalarПроверяет, является ли переменная простой.Синтаксис:bool is_scalar(mixed var)Возвращает true, если var имеет скалярный тип (чила, строки, логические значения), но не комплексный (массивы или объекты).is_nullПроверяет, является ли
1. Логические команды
1. Логические команды Наряду со средствами арифметических вычислений, система команд микропроцессора имеет также средства логического преобразования данных. Под логическими понимаются такие преобразования данных, в основе которых лежат правила формальной
Логические И и ИЛИ
Логические И и ИЛИ Вы уже видели, что такое управляющие структуры и как их использовать. Для решения тех же задач есть еще два способа. Это логическое И — «&&» и логическое «ИЛИ» — « || ». Логическое И используется следующим образом:выражение_1&&выражение_2Сначала
Логические функции
Логические функции Логические функции могут найти применение при математических, инженерных вычислениях или при сравнительном анализе данных. Мы рассмотрим одну логическую функцию на примере функции ЕСЛИ.С помощью функции ЕСЛИ вы можете создать логическое выражение и
IV. Логические операции
IV. Логические операции Обычно логические операции «считают» условные выражения операндами. Операция ! имеет один операнд, расположенный справа. Остальные операции имеют два операнда: один слева и один справа. && Логическое И: результат операции имеет значение «истина»,
Логические операции
Логические операции Логические операции выполняют над своими операндами логические функции И (&&) и ИЛИ (||). Операнды логических операций могут иметь целый, плавающий тип, либо быть указателями. Типы первого и второго операндов могут различаться. Сначала всегда
12.3.4. Логические объекты-функции
12.3.4. Логические объекты-функции Логические объекты-функции поддерживают операции «логическое И» (возвращает true, если оба операнда равны true, – применяет оператор &&, аcсоциированный с типом Type), «логическое ИЛИ» (возвращает true, если хотя бы один из операндов равен true, –
Логические операторы
Логические операторы Firebird предоставляет три логических оператора, которые могут работать с другими предикатами разными способами.* NOT задает отрицание условия поиска, к которому он применяется. Он имеет наивысший приоритет.* AND создает сложный предикат, объединяет два
Понимание истинности и ложности
Понимание истинности и ложности Семантически, если предикат возвращает «неопределенность», это не является ни истиной, ни ложью. В SQL при этом утверждения разрешаются только в виде «истина» или «ложь» — утверждение, которое не вычисляется как «истина», рассматривается как
Логические операции
Логические операции В XSLT имеются две логические операции — or и and. Эти операции бинарны, то есть каждая из них определена для двух операндов. Если операнды не являются булевыми значениями, они неявным образом приводятся к булевому типу.Семантика or и and очевидна — они
Логические операции
Логические операции К логическим относятся бинарные операции and, or и xor, а также унарная операция not, имеющие операнды типа boolean и возвращающие значение типа boolean. Эти операции подчиняются стандартным правилам логики: a and b истинно только тогда, когда истинны a и b, a or b истинно
4.1. Логические переменные и логические операции
4.1. Логические переменные и логические операции Информация (данные, машинные команды и т. д.) в компьютере представлена в двоичной системе счисления, в которой используется две цифры – 0 и 1. Электрический сигнал, проходящий по электронным схемам и соединительным
Логические нарушения
Логические нарушения Если накопитель исправен физически, но представляется как пустой или неформатированный, а находящиеся на нем данные не видны операционной системе, то в данном случае повреждены служебные таблицы файловой системы.Данные почти всегда остаются на
Логические функции в Excel
Логические функции в Excel При расчетах часто приходится выбирать формулу в зависимости от конкретных условий. Например, при расчете заработной платы могут применяться разные надбавки в зависимости от стажа, квалификации или конкретных условий труда, которые вычисляются
Как составить логическую функцию по таблице истинности
Истинность составных высказываний, образованных в результате выполнения каких-либо логических операций над простыми высказываниями, зависит только от истинности исходных высказываний. Чаще всего для установления значений сложных высказываний используют таблицы истинности.
Таблица истинности — это таблица, устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию, и значениями функции. Рассмотрим построение таблиц истинности на примере операций, рассмотренных в предыдущем разделе. Начнем с унарной операции отрицания Ā. Поскольку операция выполняется над одним операндом (A), принимающим всего два значения ( 1-истина; 0-ложь), таблица будет иметь три строки и два столбца. В заголовке таблицы укажем высказывание A и результат отрицания Ā, как показано на рисунке.
Далее в первом столбце разместим все возможные значения высказывания A, а во втором — значения логической функции Ā, как показано на рисунке.
Приведем таблицу истинности логического умножения (конъюнкции).
A B A Λ B 0 0 0 0 1 0 1 0 0 1 1 1 Заметим, что составное высказывание A Λ B истинно только в том случае, когда истинны ода высказывания и A, и B.
Таблица истинности логического сложения приведена на следующем рисунке.
A B A V B 0 0 0 0 1 1 1 0 1 1 1 1 Составное высказывание A V B ложно лишь в случае, когда оба операнда ложны.
Таблица истинности импликации, выглядит следующим образом.
A B A -› B 0 0 1 0 1 1 1 0 0 1 1 1 Составное высказывание A -› B ложно лишь в случае, когда ложь имплицируется истиной. Таблица истинности эквивалентности представлена на следующем рисунке.
A B A ~ B 0 0 1 0 1 0 1 0 0 1 1 1 Составное высказывание A ~ B истинно в том случае, когда значения операндов совпадают. Полезно иметь под рукой сводную таблицу истинности.
Сводная таблица истинности Заметим, что таблицы истинности находят широкое применение для
Два сложных высказывания называют эквивалентными , если совпадают их таблицы истинности. Высказывания, истинность которых постоянна и не зависит от истинности входящих в них простых высказываний, а определяется только их структурой, называются тождественными или тавтологиями. Различают тождественно-истинные и тождественно-ложные высказывания.
Построение СКНФ и СДНФ по таблице истинности
Нормальной форме логической формулы не свойственна эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Выделяют такие виды формы нормального типа:
- КНФ (конъюнктивная нормальная форма), где подразумевается конъюнкция того или иного количества дизъюнкций, как пример, ;
- ДНФ (дизъюнктивная нормальная форма), где осуществляется дизъюнкция конъюнкций, как пример, .
СКНФ
Совершенная КНФ является разновидностью конъюнктивной нормальной формы, удовлетворяющей такие условия:
- отсутствие одинаковых элементарных дизъюнкций;
- дизъюнкции не содержат одинаковые переменные;
- все дизъюнкции содержат каждую переменную из входящих в конъюнктивную НФ такого типа.
Так и не нашли ответ на вопрос?
Просто напишите,с чем нужна помощь
Мне нужна помощьПостроение СКНФ согласно таблице истинности
Если функция равна нулю, то в случае каждого набора записывают сумму, причем с отрицанием берутся те переменные, которые равны единице.
СДНФ
Совершенная ДНФ является разновидностью дизъюнктивной нормальной формы, удовлетворяющей следующие условия:
- отсутствие одинаковых элементарных конъюнкций;
- конъюнкции не свойственно обладать одинаковыми переменными;
в случае любой конъюнкции элементарного типа имеет место быть переменная, входящая в такую нормальную дизъюнктивную форму. При этом в одинаковом порядке.
Все формулы булевого типа, которые не относятся к тождественно ложным, могут быть представлены в совершенной разновидности ДНФ, при этом в единственном возможном варианте.
Построение СДНФ согласно таблице истинности
Если функция соответствует единице, то в случае каждого набора записывается произведение, причем с отрицанием берутся те переменные, которые равны нулю.
Нахождение СКНФ и СДНФ: примеры
Согласно таблице истинности записать логическую функцию:
Прибегнем к правилу построения совершенной ДНФ
Получаем такую СДНФ
Задействовав правило её построения:
Представить функцию как СДНФ и СКНФ, при том, что она задаётся таблицей истинности.
Для начала нужно записать логическую функцию в СДНФ. Чтобы упростить решение, добавляем к таблице столбец. Прибегнув к правилу составления СДНФ, вводим знак отрицания для переменных с нулевым значением. Инвертирование нулевых значений переменных имеет большое значение, поскольку без этого значения конъюнкций будут преобразованы в нули ключевой функции.
Вычисленные конъюнкции из вспомогательного столбца необходимо объединить знаком дизъюнкции и получим необходимую логическую функцию, имеющую вид совершенной конъюнктивной формы нормального типа:
Запишем логическую функцию в СКНФ.
Прибегнув к правилу, по которому составляется СКНФ, нужно помнить о введения знака отрицания для переменных с единицей. Инвертирование единичных значений имеет большое значение, поскольку без этого значения дизъюнкций будут преобразованы в единицы ключевой функции.
Вычисленные дизъюнкции из вспомогательного столбца необходимо объединить знаком конъюнкции, так как таким образом и можно получить необходимую логическую функцию, имеющую вид совершенной нормальной формы конъюнктивного типа.